Róg Gabriela to trójwymiarowa figura geometryczna. Ma niezwykłą właściwość: posiada nieskończoną powierzchnię, ale skończoną objętość. Wydaje się to być niezłym paradoksem, czyż nie? Oznacza to, że istnieje ilość farby, która wypełniłaby dany kielich (tudzież trąbkę), ale nie ma skończonej ilości farby, która pokryłaby całą powierzchnię kielicha (tudzież trąbki). Fajnie, nie? Tylko dlaczego? Czyż nie przeczy to zdrowemu rozsądkowi? Otóż nie. Tak jest naprawdę.
(Oczywiście pomijając drobny fakt, że w pewnym momencie cząsteczki farby byłyby za duże, by zmieścić się w coraz mniejszym otworze. Załóżmy, że tego problemu nie ma, w końcu nikt naprawdę nie stworzy nieskończonej trąbki i nie będzie nam dane zmierzyć się z tym problemem.)
W istocie ów paradoks ujawnia nam naturę nieskończoności.
Skąd nazwa "Róg Gabriela"? Sąd Ostateczny i te sprawy. Wiecie, Gabriel przyjdzie i dmuchnie w swój róg, który w swojej naturze jest łącznikiem pomiędzy boskością (nieskończoność), a szarą rzeczywistością (skończoność). W sumie, jakby sobie na serio wyobrazić jakiegoś kolesia, który gra na rogu nieskończenie długim... no cóż. Zastanawiam się tylko, czy wszystko tam w niebie jest nieskończone?
Cechy i właściwości tej figury geometrycznej zostały zbadane przez Evangelistę Torricelli. Ten fizyk i matematyk rozpoczął dyskusję nad naturą nieskończoności. Mamy puszkę farby (skończoną ilość) i nie możemy danego kształtu pomalować, bo potrzebujemy nieskończonej ilości farby, ale za to możemy dany kształt wypełnić... I pamiętajcie, że przy wypełnianiu objętości, tak czy siak pokryjemy powierzchnię całej bryły. Na "chłopski" rozum, zamalowując całą powierzchnię powinno nam zostać jeszcze trochę farby, by ją wlać do naszej trąbki. Tak się jednak nie dzieje. Sam Torricelli nie mógł w to uwierzyć - pamiętajcie, że to był XVII wiek. Dla współczesnych matematyków Róg Gabriela jest w 100% logiczny. i my sobie wytłumaczymy czemu. Droga jednak będzie kręta i wyboista.
Zacznijmy od tego, że Róg Gabriela jest powierzchnią obrotową, czyli taką, którą tworzy się poprzez obrócenie wokół osi dwuwymiarowej krzywej. Do figur w ten sposób wytworzonych można zaliczyć jabłko, stożek, sferoidę, pseudosferę, cytrynę.
Konkretniej: Róg Gabriela jest powierzchnią (bryłą) obrotową funkcji hiperbolicznej y=1/x, gdzie x
*
Tak wygląda funkcja y=1/x. Proszę zauważyć, że poszczególne "końce" funkcji zmierzają, dążą, chcą się zbiec do odpowiednio osi y (obie strony, dodatnia i ujemna) i jednocześnie do osi x (obie strony), przy czym nigdy, ale to nigdy nie przetną tych osi - będą w nieskończoność dążyły, żeby, jak najbliżej się złączyć, ale nigdy nie złączą. To się nazywa asymptotą - prosta do której zmierza funkcja. Są trzy rodzaje asymptot: pionowa, pozioma i ukośna, dodatkowo pośród nich można wyróżnić lewo-, prawostronną oraz obustronną. Funkcja y=1/x posiada dwie asymptoty y=0 i x=0, są one obustronne. Tworząc Róg Gabriela odcinamy całą część wykresu, która jest mniejsza od x=1, obracamy tę krzywą, dzięki temu tworzy nam się figura o kształcie rogu.
Jak to możliwe, że wlewając farbę do tego stożka jesteśmy w stanie pokryć jego wewnętrzną powierzchnię, a nie możemy pokryć zewnętrznej warstwy malując super-ultra-hiper cienką warstwą farby? Oczywiście farba jest tylko tutaj narzędziem: nie bierzmy tej gimnastyki myślowej tak dosłownie: jak już wspominałam, w końcu tak, czy siak pojedyncze cząsteczki farby nie będą mogły wejść w wąską średnicę naszej zwężającej się tuby.
Zacznijmy od ... Euklidesa. Geometria Euklidesowa, opisana przez faceta o tym samym imieniu (Euklides się zwał - przypadek, nie sądzę) i napisana dawno, bardzo dawno, bardzo dawno temu. III wiek przed urodzeniem tego lewaka, Chrystusa. Czasy rozkwitu cywilizacji śmierci, jaką z pewnością reprezentowała starożytna Grecja (Jezus jeszcze nie umarł za ich grzechy) były jednocześnie czasami rozwoju nauki i sztuki. Euklid również przyczynił się do tego, wynajdując nowy sposób myślenia, który można określić, jako metodę hipotetyczno-dedukcyjną (Holme, 2002, strona 68).
Euklid oparł swoją geometrię na 5 aksjomatach (oczywistości, których nie trzeba udowodniać) i 5 postulatach (już trzeba trochę bardziej udowadniać).
Do 5 aksjomatów zaliczamy:
- Wyrażenia, które są równają się temu samemu wyrażeniowi, są sobie równe.
- Jeżeli równania dodawane są do równań, wtedy całości są sobie równe.
- Jeżeli równania odejmowane są do równań, wtedy całości są sobie równe.
- Wyrażenia, które się pokrywają, są sobie równe.
- Całość jest większa od części.
- Dowolne dwa punkty można połączyć odcinkiem.
- Dowolny odcinek można przedłużyć nieograniczenie (uzyskując prostą).
- Dla danego odcinka można zaznaczyć okrąg o środku w jednym z jego końcowych punktów i promieniu równym jego długości.
- Wszystkie kąty proste są przystające.
- Dwie proste, które przecinają trzecią w taki sposób, że suma kątów wewnętrznych po jednej stronie jest mniejsza od dwóch kątów prostych, przetną się z tej właśnie strony.
Książki Euklidesa opisujące "jego" geometrię były niezwykle poważane przez setki lat do tego stopnia, że tuż po wynalezieniu druku, "Elementy" (jego dzieło opisujące geometrię; składająca się z 13 książek) stały się pierwszą matematyczną wydrukowaną serią. Ogólnie wpływ "Elementów" znacznie wykraczał poza świat naukowców i matematyków. To dzieło dosłownie kształtowało myśli ludzi i miało wpływ na to, jak widzą świat. Zakwestionowanie tego wszystkiego mogło mieć poważne konsekwencje i spotkać się z ogólnym ostracyzmem.
Pierwszą kontrowersje odnośnie geometrii Euklidesa zaczęły się pojawiać w momencie, gdy okazało się, że piąty postulat Euklidesa nie zawsze działa. W tym tekście na stronie 6 jest napisane:
"Indeed, controversy arose when a group of young mathematicians revealed that Euclid’s fifth postulate is not always true or not true at all. This postulate had long been considered to have something that is not quite true. Greeks writers had tried to give a more rational explanation of it but failed (Gray, 2004, p. 20). Also, O’Shea (2007) pointed out that the length of the fifth postulate compared to the four other ones might suggest that even Euclid knew about the ambiguity of that postulate; therefore, he took more time to explain it (p. 57). One needs to know that the fifth postulate is central to Euclid’s Elements; without it, a great part of his logical body of mathematics would not have existed. For example, the parallel postulate is used to demonstrate the Theorem of Pythagoras, which states that the square of the greater side in a right triangle is equal to the sum of the squares of the two other sides; also, the theorem that the sum of the angles in a triangle is exactly two right angles and the construction of similar triangles depend exclusively on the fifth postulate (Gray, 2004, p. 19-20). Those three young mathematicians, Johann Carl Friedrich Gauss (1777-1855), Nikolai Ivanovich Lobachevsky (1792-1856), and Janos Bolyai (1802-60) brought a significant contribution to challenge the fifth postulate (O’Shea, 2007, p. 62). Those brilliant men discovered that other geometries were consistent without the fifth postulate; those geometries, under a generic name of non-Euclidean geometry, are usually called elliptic geometry, spherical geometry, and hyperbolic geometry."
Ten piąty postulat jest istotny i ważny. Z niego, albo raczej z "usunięcia" go, powstaną później podstawy do geometrii innej, niż Euklidesowa. Należy pamiętać, że w geometrii Euklidesowej do stworzenia figur, brył, zależności używa się podstawowych konceptów: punktów, linii, powierzchni. Usunięcie, tudzież zmiana postulatu 5 pozwala nam na tworzenie zupełnie innych figur.
Aby całkowicie wyjaśnić sobie sprawę z geometrią euklidesową zaczerpnijmy trochę wiedzy z polskiej Wikipedii:
"Wyjątkowość piątego postulatu wynikała z tego, że od początku wydał się bardziej skomplikowany od pozostałych[a]. Nasuwało to podejrzenia, że może on być wnioskiem z pozostałych, bowiem zgodnie z ówczesnymi wyobrażeniami każdy postulat powinien być prosty i oczywisty. Ponieważ piąty postulat nie był ani prosty, ani oczywisty, całe pokolenia matematyków próbowały go dowieść na podstawie pierwszych czterech. Wszystkie te próby – choć nie mogły się powieść – walnie przyczyniły się do uściślenia pojęć, wysublimowania metod dowodowych. Było to zagadnienie wytyczające przez wiele wieków kierunki rozwoju geometrii.
Na początku XVIII w. matematycy jak dotąd bezskutecznie zmagający się z problemem piątego postulatu zmienili podejście: zamiast podejmować kolejne próby jego dowodzenia, zaczęli starannie wyodrębniać twierdzenia wynikające z wyłącznie pierwszych czterech postulatów, a dołączając zaprzeczenie piątego postulatu, starali się uzyskać sprzeczność. Nieświadomie stworzyli przy tym podwaliny geometrii absolutnej, czyli geometrii opartej na pierwszych czterech postulatach Euklidesa. Największe zasługi mają tutaj Giovanni Gerolamo Saccheri[b] i Lambert[c].
Przez wiele lat podejmowane nieskuteczne próby znalezienia sprzeczności zrodziły najpierw podejrzenia, a potem przekonanie, że takiej sprzeczności po prostu nie ma, a teoria z zaprzeczonym piątym postulatem jest jak najbardziej poprawna (Gauss, Bolyai, Łobaczewski). Stworzenie przez Kleina modelu dla takiej teorii definitywnie zamknęło problem – aksjomat ten okazał się niezależny od pierwszych czterech.
Współcześnie geometria absolutna jest teorią, która ma dokładnie dwa rozszerzenia do teorii kategorycznej w zależności od tego, czy dołączy się do niej aksjomat Euklidesa o równoległych czy też jego zaprzeczenie. W pierwszym przypadku jest to geometria euklidesowa, w drugim – geometria hiperboliczna.".
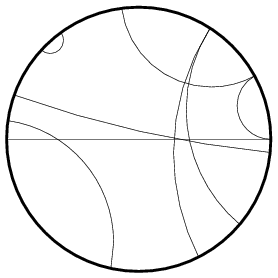
Geometria nie-Euklidesowa (sferyczna, hiperboliczna, eliptyczna - przestrzenie zakrzywione)
Od lewej: geometria euklidesowa, sferyczna i hiperboliczna. Interpretacja powierzchni, punktu, prostej i kąta.
Napisałam wyżej, że geometria Euklidesowa składa się między innymi z prostych. Jak widać na ostatnim obrazku kąt pomiędzy dwiema prostymi jest prosty. Piąty postulat mówi o tym, że jeśli ten kąt będzie mniejszy, niż 90 stopni, to dwie proste przecięte przez trzecią (tę środkowa na obrazku; z którą przynajmniej jedna prosta tworzy kąt mniejszy, niż 90 stopni) w końcu przetną się. Jak widać w geometrii hiperbolicznej i eliptycznej ten postulat nie działa. Dlaczego? Odpowiedź jest prosta: geometria hiperboliczna różni się tym od euklidesowej, że nie ma w niej linii prostych - są za to krzywe. Punkt oznacza to samo w obu geometriach, ale prosta nie. Pamiętacie pewnie, że nazwałam funkcję y=1/x hiperboliczną. Oznacza to, że Róg Gabriela nie wywodzi się z geometrii Euklidesowej i nie wszystkie aksjomaty, tudzież postulaty obowiązują go.
Zakładając hipotetycznie, że postulat 5 jednak działa w rogu Gabriela oznacza to, że...
... dwie funkcje tworzące dany róg (jego granice) w końcu by musiały się spotkać. W związku z tym róg miałby skończoną objętość i powierzchnię, no ale jak wiemy, tak nie jest. Ze względu na to, że w wielu przypadkach objętość i powierzchnia są ze sobą ściśle związane, uczeni myśleli, że skoro powierzchnia jest nieskończona, to objętość też musi być. Tak się jednak nie dzieje.
Zanim przejdziemy dalej, bezpośrednio do rogu Gabriela, zgłębmy się bardziej w geometrię nie-euklidesową. To wyjaśni nam lepiej, czemu Róg Gabriela ma takie, a nie inne właściwości.
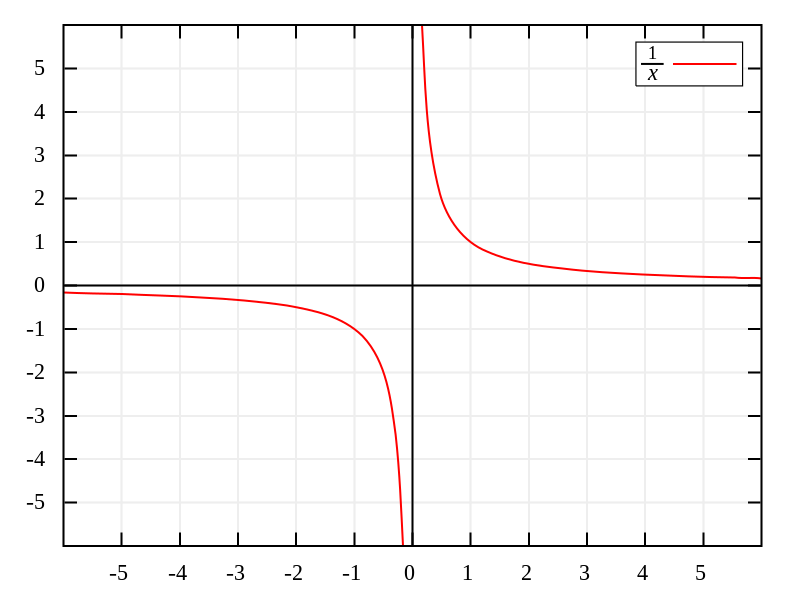
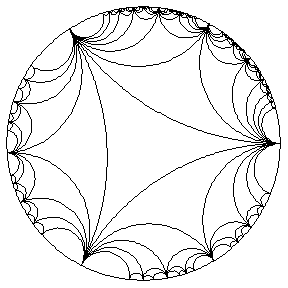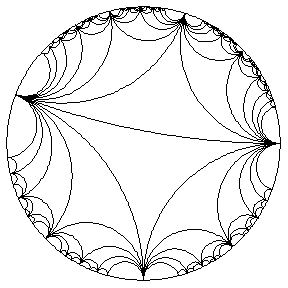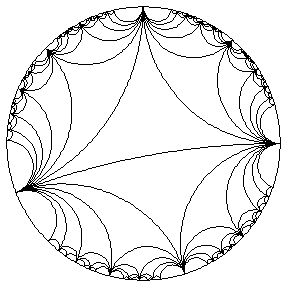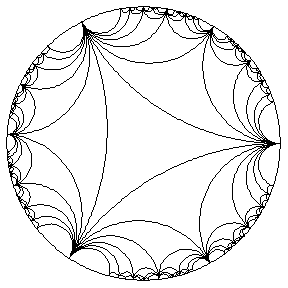
Model dysku Paincare
Zwróćcie uwagę na trójkąt po prawej stronie.
Funkcja y=1/x ma ona asymptoty w x=0 i y=0 i nigdy nie osiągną poziomu tych osi - będą w nieskończoność "lecieć", ale nigdy nie przekroczą magicznej granicy 0. To samo dzieje się w tych okręgach - linie wewnątrz nich nigdy nie dosięgną tych granic, choćby nie wiem co! W pewnym sensie granice okręgu są asymptotami. Linie są coraz "mniejsze" im bliżej granicy okręgu się znajdują. Wyobraźcie sobie, że patrzycie w rzeczywistości nie na okrąg, a na figurę 3D, której podstawą jest koło, a której środek jest bardzo blisko Was, a rozchodzi się ona jednocześnie we wszystkie strony (tworząc ów podstawę o kształcie okręgu) w nieskończoną odległość przed Wami. Szczególnie widać to w 1, 2 i ostatnim obrazku.
W gifie widać charakterystyczne "trójkąty", kazałam Wam też zwrócić uwagę na nie na kolorowym obrazku. Są to tak zwane trójkąty asymptotyczne, w przypadku gifa ruchomego jest to trójkąt potrójnie asymptotyczny. Wyobraźcie sobie normalny, zwykły trójkąt, jednak zamiast utworzyć kąty, których suma równa się 180 stopni, dwie proste stają się równoległe i dążą do nieskończoności. Suma kątów w tym trójkącie jest mniejsza, niż 180 stopni.
Trójkąt asymptotyczny. Trójkąt potrójnie asymptotyczny będzie miał wszystkie "rogi" leżące na dolnej linii, zwanej absolutem, bowiem symbolizuje ona nieskończoność.
Te charakterystyczne "półkola" w okręgu mają środek na osi x i "przestrzegają" one wszystkie postulaty Euklidesa oprócz 5. Zobrazowanie ich nazywa się modelem półpłaszczyzny Poincarego.
Dla nas najważniejsze są ów trójkąty. Powierzchnia rogu Gabriela jest dwuwymiarowa, dlatego że możną ją "zaprezentować" dwoma wektorami. Składa się ona z trójkątów asymptotycznych. Myślę, że to całkiem logiczne, jeśli macie cały czas w pamięci, pewien fakt, że Róg Gabriela jest funkcją hiperboliczną y=1/x, która dąży do 0, ale nigdy go nie przekroczy i im dalej x, tym bardziej bliżej samej osi x (bliżej 0; to samo tyczy się oczywiście -x, oraz obu stron y, jednak dla Rogu Gabriela bierzemy pod uwagę tylko x>=1, po to właśnie, żeby uniknąć wielkiego wiru długości nieskończoności, który dotyka powierzchni również nieskończenie wielkich rozmiarów.
Powierzchnią Rogu Gabriela jest suma powierzchni trójkątów asymptotycznych, zatem jest ona nieskończona. Skoro powierzchnia Rogu jest nieskończona, to czemu objętość jest skończona? Tutaj nie ominiemy matematyki, jako, że wynika to ściśle z równań. Jeśli rozumiecie granice, z łatwością zrozumiecie, czemu jest tak, a nie inaczej.
Równanie powierzchni:

Równanie objętości:

W momencie, gdy a dąży do nieskończoności objętość dąży do pi

Natomiast jeśli chodzi o powierzchnię, to spójrzmy na jej równanie, w którym jest logarytm naturalny. Nie ma górnej granicy dla tej funkcji.
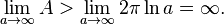
Ktoś może powiedzieć, że Rogu Gabriela nie da się stworzyć w rzeczywistości, ale jest to twierdzenie bezzasadne i niepoparte niczym. Pojęcie nieskończoności po dziś dzień zajmuje matematyków, a Róg Gabriela, albo raczej jego cechy, wykraczają poza nasze intuicyjne rozumowanie, co nie oznacza, że nie mógłby on istnieć. Równie dobrze można powiedzieć to samo o teorie względności, a przecież wiadomo, że jest ona naprawdę i sprawdza się w rzeczywistości. To, co robi matematyka, tudzież fizyka, można porównać z badaniem anomalii medycznych i genetycznych wad: poprzez badanie innych rzeczy, niż nam znane, poprzez zbadanie "innego", mamy odniesienie do naszej komfortowej rzeczywistości. Dzięki temu możemy nie tylko lepiej ją pojąć, ale także nabrać do niej dystansu... a także do siebie samych.
P.S. Będę szczera, jak szukałam wiadomości odnośnie Rogu Gabriela myślałam, że jego natura będzie bardziej skomplikowana. Po odnalezieniu równań (granice), które prowadzą do konkluzji: objętość policzalna, powierzchnia niepoliczalna, myślę sobie NO K^%$# OCZYWIŚCIE. I byłam bardzo, ale to bardzo rozczarowana. Jak mogłam się tak nabrać, że to "nie wiadomo co" jest! Tak bardzo rozczarowana, że aż poczułam obrzydzenie! Nie wiem czemu! Chyba na siebie, że się tym tak podnieciłam!









Myślałaś, że złapałaś Absolut za jego nieskończony róg, a tu... ni chuja ;D
OdpowiedzUsuńA tak poważnie, rzeczywiście, ciekawa rzecz. Bez znajomości matematyki ktoś mógłby zacząć twierdzić, że naprawdę mamy tutaj dowód na istnienie Boga.
No tak, to w sumie oczywiste, skoro obracamy funkcję posiadającą asymptotę. W takim wypadku asymptotą staje się objętość (ograniczenie zmienia się z 2D do 3D w wyniku obrotu), a długość półprostej jak była, tak pozostaje nieskończona, tylko wyraża się powierzchnią. Czepianie się tego tworu to faktycznie jak czepianie się wykresu samej funkcji, który z jednej strony jest nieskończenie długi, ale z drugiej zbliża się zawsze do określonej prostej - to dokładnie taki sam "paradoks", tylko w przestrzeni. W znanej nam naturze problem rozwiązuje się sam, jak zostało to zauważone w tekście. :P Właściwie wyobrażenie sobie skończonej objętości zmieniającej się w nieskończoną powierzchnię to żaden problem. Weźmy sobie sześcian, który "spłaszczamy" w nieskończoność, powodując zwiększanie powierzchni jego podstaw, kosztem wysokości (objętość constant). W ten sposób (gdyby nie wielkość atomów) również zmierzalibyśmy do nieskończonej powierzchni pomalowanej skończoną objętością farby, która mogłaby znajdować się we wnętrzu sześcianu na początku procesu "spłaszczania". Dobrze rozumuję? :P
OdpowiedzUsuń